Ихэр анхны тоонууд

Ихэр анхны тоонууд гэдэг нь зөрүү нь 2 байх 2 анхны тоон хосыг хэлнэ. Жишээлбэл, 3 ба 5, 11 ба 13, 857 ба 859-ууд нь ихэр анхны тоонууд болно.

Анхны тоонууд төгсгөлгүй олон болох нь Эртний Грек үед мэдэгдэж байсан боловч ихэр анхны тоонууд төгсгөлгүй олон эсэх нь одоо болтол тодорхойгүй.

Гэхдээ одоогоор олдоод хамгийн том анхны ихэр тоонууд нь 58711 оронтой юм байна. 

Энэ тоо юм. Эдгээр нь 2007 оны 1 сард олдсон байна. (※2,003,663,613 = 3 × 7 × 487 × 195919)

Ихэр анхны тооны шинжүүдээс: 

• 3-с бусад бүх ихэр анхны тоонууд нь 6n - 1 буюу 6n + 1 хэлбэрээр илэрхийлэгдэнэ. Энд n нь мэдээж натурал тоо.
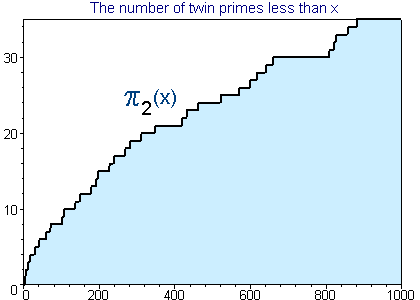
• x-с бага ихэр анхны тоонуудын тоо нь хамгийн ихдээ O(x/(log x)²) болно. Иймд p ба p + 2 нь анхны тоонууд гэж үзвэл:

• (Бүх ихэр анхны тоонуудын урвуунуудын нийлбэр) нь нийлнэ (Брун, 1919). Энэхүү нийлбэр （1.90195……）-ийг Бруны тогтмол гэнэ.
• p + 2 нь хамгийн ихдээ 2 ширхэг анхны тооны үржвэр хэлбэрт тавигддаг анхны тоо p нь төгсгөлгүй олон оршин байдаг (Чен Жинг Рун, 1966).
• Бүхэл тоо n ба n + 2 нь хоёул анхны тоо байхад л 4 [(n - 1)! + 1] + n ≡ 0 (mod n(n + 2)) тэнцэтгэл биелнэ. (Клемент, 1949).
• 2005 онд Даниел Голдсон дараах тэнцэтгэлийг баталсан:

   

"Proof of Infinitely many Twin Primes" - Ихэр анхны тоонууд төгсгөлгүй олон болохыг баталсан бүтээл. Хожим нь энэ бүтээл алдаатай болох нь илэрсэн.